K-Core

Coreness is a measure that can help identify tightly interlinked groups within a network. A k-core is a maximal group of entities, all of which are connected to at least k other entities in the group.

K-Core is a measure that can help identify small interlinked core areas on a network. To be included in the K-Core, an entity must be linked to at least k other entities in the group. The linked entities are regardless of how many other entities that they are connected to outside of the group. Maximal in the definition means that we are interested in the largest set of entities with the required minimum number of neighbors within the group. The value of k is sometimes referred to as the coreness of the group.

For example, a group is the two-core if it contains all entities that are connected to at least two other entities within the group. Similarly, a group is the three-core if it contains all entities that are linked to at least three other entities within the group.

Any entity in the three-core must have at least three links to all other members of the three-core. Clearly any such entity must necessarily have at least two links to every other member of the three-core. Put another way, the three-core is a subset (is contained within) the two-core. More generally, the K-Core form a nested hierarchy of entity groupings on the chart. The zero-core (entire chart) contains the one-core, which contains the two-core, which contains the three-core, and so on. As k increases, the core sizes decrease, but the cores become more interlinked. The K-Cores with the biggest coreness values (k-values) represent the most cohesive regions of the chart.

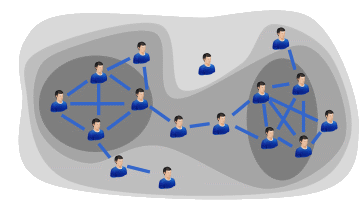
The following diagram illustrates the K-Core decomposition of a simple network, and shows a nested collection of zero, one, two and three-cores. Notice that the three-core actually consists of two separate groupings on the chart. Technically these groupings are regarded as a single three-core with two components.